This article was inspired by this LinkedIn post by Fermat’s Library.
You would have all heard about the Fibonacci series – 1, 1, 2, 3, 5, 8,… Each number in the sequence is obtained by adding the previous two numbers. Tribonacci series is similar, but instead of adding the previous two, we add the previous three.
The Tribonacci series is 1, 1, 2, 4, 7, 13, 24, 44, … We are interested in finding the ratio of the nth term in the series to the (n+1)th term.
Let a_n be the nth term of the Tribonacci series.
a_n = a_{n-1} + a_{n-2} + a_{n-3}Divide both sides by a_{n-1},
\frac {a_n} {a_{n-1}} = 1 + \frac {a_{n-2}} {a_{n-1}} + \frac {a_{n-3}} {a_{n-1}}
Let the limiting ratio \frac {a_{n-1}} {a_{n}} be x.
x = \lim\limits_{n \to \infty} \frac {a_{n-1}} {a_n} \therefore \frac 1 x = 1 + x + \lim\limits_{n \to \infty} \frac {a_{n-3}} {a_{n-1}} \implies \frac 1 x = 1 + x + \lim\limits_{n \to \infty} \frac {a_{n-3}} {a_{n-2}+a_{n-3}+a_{n-4}} \implies \frac 1 x = 1 + x + \lim\limits_{n \to \infty} \frac {1} {\frac {a_{n-2}}{a_{n-3}} + 1 + \frac {a_{n-4}}{a_{n-3}}} \implies \frac 1 x = 1 + x + \frac {1} {(\frac 1 x + 1 + x)} \implies (\frac 1 x - 1 - x) (\frac 1 x + 1 + x) = 1 \implies (1 - x - x^2) (1 + x + x^2) = 1 \implies 1 - 2x^2 -2x^3 - x^4 = 0 \implies (x^3 + x^2 + x -1) (x + 1) = 0Obviously, x \ne -1 . Hence, x must be the real solution to the equation:
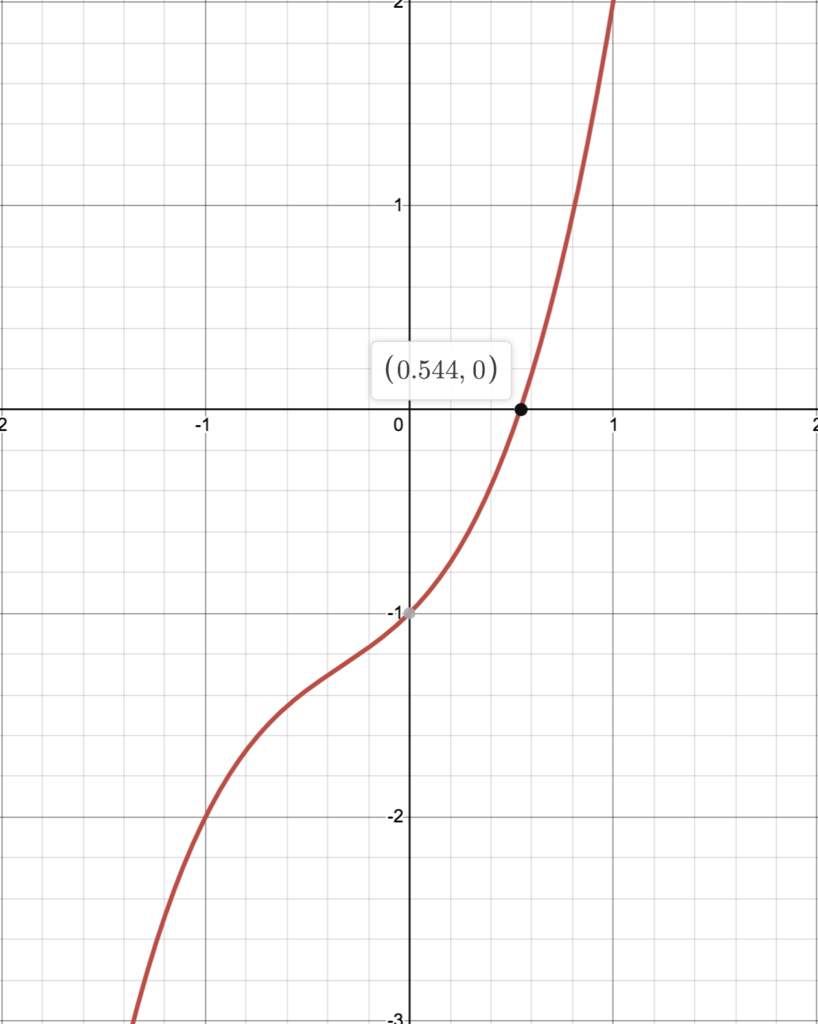
\implies (x^3 + x^2 + x -1) = 0Following is the graph of y = x^3 + x^2 + x -1 (Desmos Link). As we can see, the real root is at x \approx 0.544
Let us check if it indeed is true using the first few terms, 1, 1, 2, 4, 7, 13, 24, 44, …
| a_{n-1} | a_n | \frac {a_{n-1}} {a_{n}} |
| 1 | 1 | 1 |
| 1 | 2 | 0.5 |
| 2 | 4 | 0.5 |
| 4 | 7 | 0.571 |
| 7 | 13 | 0.538 |
| 13 | 24 | 0.542 |
| 24 | 44 | 0.545 |
| 44 | 81 | 0.543 |
| 81 | 149 | 0.544 |
We can indeed verify that it converges to 0.544.
General Solution for ‘k’th Order Fibonacci Ratio
The above solution need not be complex, as I had overlooked the fact that
\frac {a_{n-p}} {a_{n-1}} = \frac {a_{n-p}} {a_{n-p-1}} . \frac {a_{n-p-1}} {a_{n-p-2}} ... \frac {a_{n-2}} {a_{n-1}} \implies \frac {a_{n-p}} {a_{n-1}} = x^{p-1}Therefore, for a ‘k’th order Fibonacci sequence,
a_n = a_{n-1} + a_{n-2} + a_{n-3} ... a_{n-k}Divide both sides by a_{n-1},
\frac {a_n} {a_{n-1}} = 1 + \frac {a_{n-2}} {a_{n-1}} + \frac {a_{n-3}} {a_{n-1}} ...\frac {a_{n-k}} {a_{n-1}} \implies \frac 1 x = 1 + x + x^2 + ... + x^{k-1}Hence, x is the value for which this iteration converges:
x = \frac 1 {\sum_{i=0}^{k-1} x^i}It is the value of the real root of
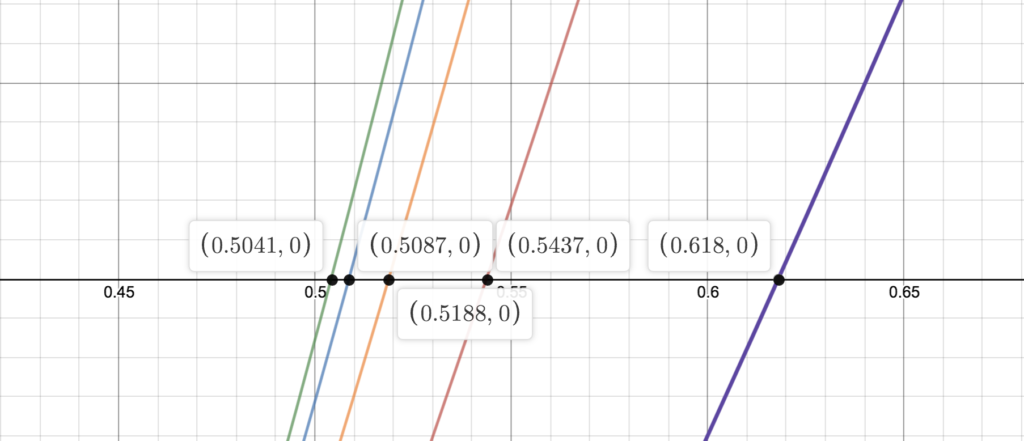
x^k + x^{k-1} + x^{k-2} + ... + x -1 = 0The following plot shows the roots for k=2 to k=6. It is interesting to observe that for k=2, the root is 1 over golden ratio \frac 1 {\phi} = 2/(1+\sqrt{5}) \approx 0.618 . For k=\infin, the root is 0.5.